Why are rivers so difficult? Because they do so many things. It's easy to recognise that rivers tend to start on high ground and flow downhill until they reach the sea. But they also meet with each other; flow into lakes and then out of them again; erode material from under and around them; deposit material around and under them; meander; flood; split up (occasionally) and form deltas. All of these things are a nightmare to model. Unless you're directly modelling the movements of billions upon billions of water droplets and soil particles in a full physics simulation, you're going to have to simplify these processes and live with some inaccuracy.
So in that spirit, let's think about how to do this. It seems to me that there are two basic ways to do rivers. The first is to think of rivers as discrete things that flow over the ground. To create rivers, we start at some relatively high point and then draw the river along the rest of its course until we reach the sea. (Or you can, more counter-intuitively, start from the river mouth and then draw the river upwards, branching as you go, until you reach the source, as Zhang et al. do.) Initially, I tried doing it this way, from source to mouth. I plonked river sources high up and tried to make the computer trace their paths downhill. An immediate problem with this is that sometimes there isn't a downhill - sometimes the river reaches a flat point. Then you need to program ways to make it try to find a route that look realistic. This is difficult, and I couldn't get decent results. My rivers kept on running across valleys and smashing into the hills on the other side.
Luckily I then stumbled across Martin O'Leary's method, which is the second way to do rivers. With this approach, you forget about rivers for the time being and think instead about the flow of water over all of the ground. Suppose that every land cell of the map has a direction of flow and a size of flow. All you have to do is work out how much precipitation falls on each cell (we know that already), and add that amount to the cell it's flowing to, and then add that to the cell is flowing to, and so on. That allows you to map out a complete map of water flow, and you can mark all tiles that have more than a certain amount of flow as rivers.
That sounds simple, but of course it faces the same problem of flat areas, where it's not clear where the cell should flow to, and (worse still) depressions. A depression is an area of land that is entirely lower than the border around it. In the real world, if a river flows into a depression, it would normally fill it up to make a lake, and then flow out of the other side. This is surprisingly difficult to simulate. Fortunately, we can avoid it if we simply eradicate all depressions before making the rivers. O'Leary once again provides the solution: the Planchon-Darboux algorithm, which is a method of doing precisely this - it goes over a heightmap held in an array and fills in the depressions. Not only that, but it adds a slight, regular slope to all the flat surfaces, meaning that every land cell on the map now has at least one neighbouring cell that is lower than it. There are actually a number of algorithms for doing this, some of which - such as Wang-Liu - are faster than Planchon-Darboux. But they are difficult to implement, at least for me. Whereas Planchon and Darboux's paper is not only readable even by a humanities scholar like me, but they provide pseudo-code that isn't too hard to adapt.
So I wrote an adaptation of this algorithm and added it to the end of the terrain generation, before the climate modelling starts. Now you may remember, when I described the mountain system, that I said that Undiscovered Worlds retains two world terrain maps: one with mountains and one without. The one with mountains is what we've been using to calculate precipitation and temperature. But we're applying the depression-filling algorithm to the one without mountains, because that's the one we're going to use for rivers. That might seem crazy, because surely we want rivers to react to mountains! Yes, we do, but remember that when we did the mountains we also raised the terrain underneath them on the no-mountains map. It's just not raised all the way to the height of the actual mountains. That means that, wherever there are mountains, the corresponding cells on the no-mountains map will still have raised land. And that means that when we do our rivers, they will react to it.
The reason why we need to do it this way should be obvious: suppose you have an area of the map with mountain ranges all around. If we do a depression fill on the map with mountains, we'll fill that area up, creating an incredibly high plateau that will look very unrealistic. If we confine our depression fill to the no-mountains map, then the area will get filled up, but not to the tops of the mountains. So it will look much more believable.
So, if we apply this to the map we've been developing, we get this:

You can see that the terrain looks much flatter than it did before, as all those depressions and hollows have gone, to be replaced by gently sloping plains.
Now we can work out the water flow! We'll have a new array for this, mapping onto the whole global map, which will store three values for each cell: the direction of flow from that cell (in one of eight directions - N, NE, E, SE, S, SW, W, NW - cells in the UW world are considered to adjoin to all eight of their neighbours); the amount of water flowing through that point in January; and the amount of water flow in July (both measured in cubic metres per second).
First, we go through the map and work out the direction of flow for each cell on the land. That's easy - we just have to find the lowest neighbouring cell and record its direction.
Then, we go through the map again and work out the flow amount for each cell on the land. For each point, we find the precipitation for that cell (for both January and July) and convert that into the amount of flow it would generate, using a highly scientific conversion formula that I made up and kept tinkering with until it seemed to yield roughly the amount that looked vaguely right. We add that amount to the flow for the cell in question. Then we move to the cell that it's flowing towards (which is easy, because we worked out what that was and stored it earlier), and add the same amount of flow to that cell. We keep doing that until we reach the sea. And we do this for every cell on the land.
Once we've done that, we have a map of flow right across the world. And we can display rivers simply by making the computer mark any cells that have flow over a certain amount. In fact it's easy to show the relative sizes of river by drawing the higher flows in darker blue and the lower ones in lighter. And so, the moment of truth - our river map:
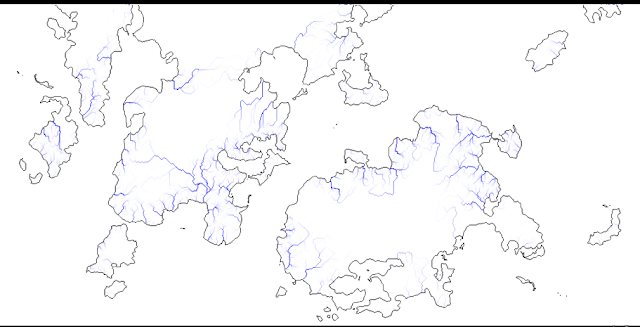
Well... it's a start. We have a recognisable river network, and they are clearly starting from high ground and working their way to the sea. They meet and merge, creating nice branching systems. We also have some interesting patterns emerging - I especially like that very long river on the northern continent that starts in the mountains near the western coast but flows southeast all that way (mostly through desert, if you compare the climate map in the last post). But there are also some serious problems here. There are an awful lot of straight lines, which look horribly unnatural. The rivers don't seem to like changing direction at all unless they really have to, and when they do they seem to bend at right angles and then go straight again. The result is quite an artificial-looking map.
What's gone wrong? It's partly the result of the way the Planchon-Darboux algorithm works. It applies a steady increment (e, in the original paper, if you're interested) to flat surfaces to create its slopes. That means that once a flow system is on that slope, it just slides down it without deviating until it hits some feature that was there before Planchon-Daboux got to work. In O'Leary's implementation, where I got this idea in the first place, this didn't matter, because he uses Voronoi cells. The great advantage of Voronoi cells is that they split the map up into tiny irregularly-shaped elements, and that means that even "straight" lines, like those created by water flow in this simulation, don't actually look straight on the map. As discussed before, by using traditional arrays instead of Voronoi cells we retain much more control over the details of the world simulation, but we pay for that by being susceptible to unpleasant artifacts like this, because we're effectively using a giant chessboard.
Well, one way to address this is by tinkering with the Planchon-Darboux algorithm itself. As I just said, it applies a steady increment to its surfaces. What if we make that increment unsteady, so that it's a random amount (within reason) for each cell where it's done? We can't allow it to get too high, or the whole map will be covered in towering plateaux, but a little variation might help. So I tried making a noise array to modulate e throughout the function, and ran it again:
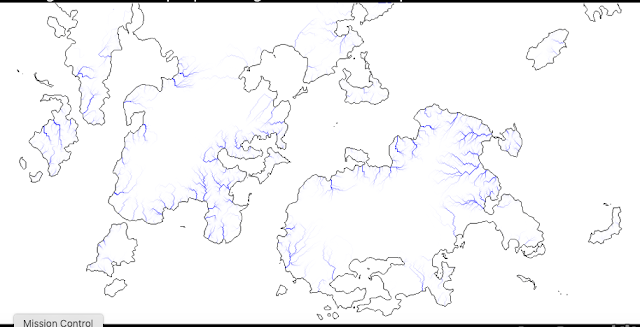
This is an improvement. That nice long river on the northern continent has disappeared - no doubt its flow got somehow diverted in the shake-up, but that's not important. In general, these rivers look wigglier and curvier than the ones we had before.
There are still some annoying flaws, though. You can see that some of the rivers still have some rather angular corners in them, and a tendency to run too straight. And when I came to do the regional maps, I found that the ways they join up don't look brilliant - in particular, tributaries often meet larger rivers at right angles, when they ought really to be already turning in the same direction as the larger river before they meet (at least most of the time). Also, there is too much of a tendency to have rivers running parallel to each other for long distances without meeting, which doesn't look natural. So I made further changes to the global river calculations. First, I added a function that adds a bit more noise to the whole map - raising and lowering random points by a small amount - after the modified depression-filling algorithm. Then I made it call the depression-filling algorithm again (because that process might have created new depressions).
Then I made some changes to after the point at which UW works out the flow directions, but before it works out the flow volumes. Now it does some further tinkering with the flow directions. It goes over the whole map and forces tributaries to turn in the direction of their destination rivers before hitting them, and it forces flows that run parallel to each other for a while to merge. This sometimes means altering the height of some cells, and it sometimes means that cells flow into a neighbouring cell that, although lower, isn't the lowest neighbouring cell. That's not totally realistic, because water always flows down the steepest available slope. However, I think we can get away with it. Remember that each cell on this map is 32 km across. Even if one 32 km sq area is, on average, higher than a neighbouring one, it's perfectly plausible that there might be a lower route through it that the river is taking.
All of that was incredibly tedious and tricky to do, but I think it helped. So here's the final river map, after all of those tweaks:
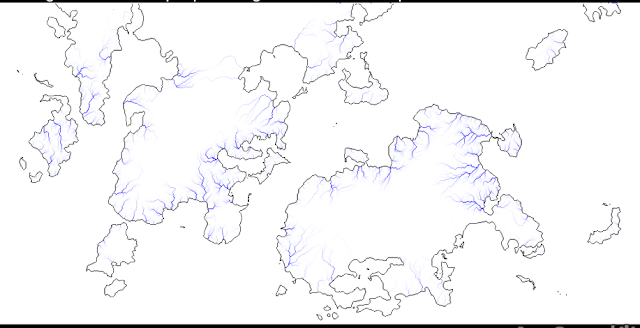
And I think that looks pretty reasonable. Of course we can't see the details of the rivers very well at this scale, but this provides us with a good framework for creating the rivers on the regional maps when we get to that stage.
You'll notice that I've said nothing about erosion in all of this. That's deliberate, because of the scale we're dealing with here. Look at a map of the whole world: you won't, for the most part, see any obvious river valleys or estuaries. They are simply too small-scale to see on a global map. So I'm assuming that, on the global map, there is no discernible erosion; we can get away with imagining that rivers simply flow over the land as if it's made of plastic and don't alter it in any way. Of course we won't be able to get away with that at the regional level. Making rivers at the regional level is going to be fun.

No comments:
Post a Comment